Senior Projects 2020
Beth Root - The Cyclic Cutwidth of Cartesian Product Graphs, Advisor Dr. Eric Bucher
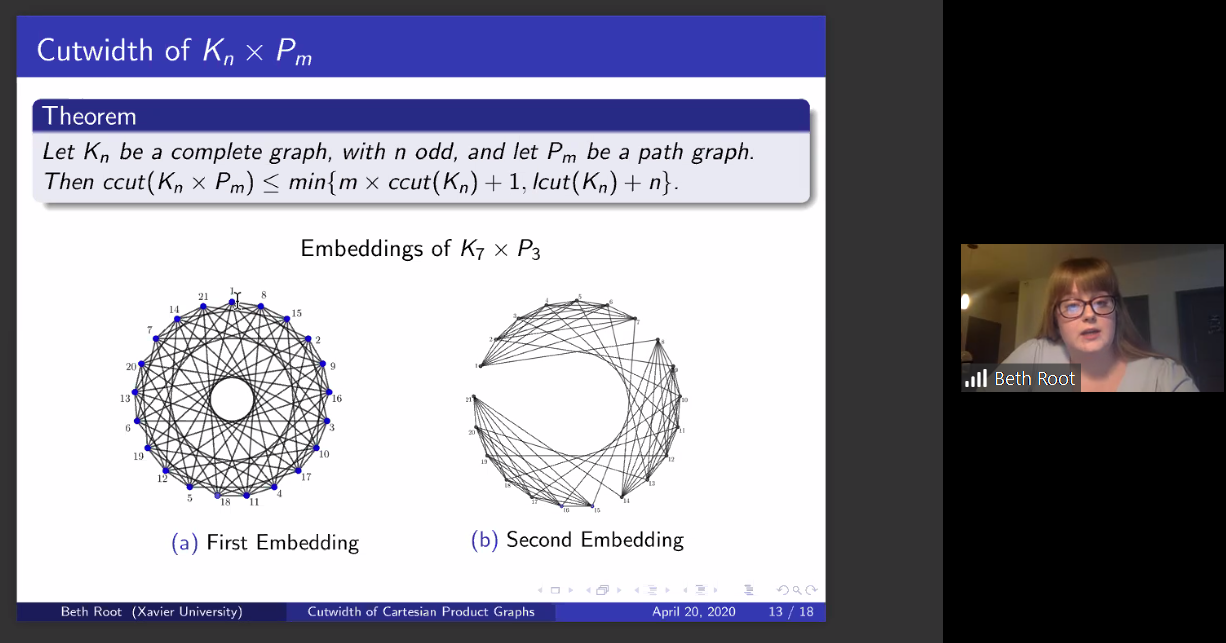
In this presentation, we will look at the cyclic cutwidth of varying families of graphs. Specifically, graphs created from the Cartesian product of paths, cycles, and complete graphs. The cyclic cutwidth of a graph can be thought of as identifying the vertices of a graph on a cyclic embedding such that the length of the longest edge is minimized. The minimum cutwidth of all possible cyclic embeddings is the total cyclic cutwidth of the graph. Through this, we have defined theorems for the cyclic cutwidth of the Cartesian product of paths, cycles, and complete graphs which we will elaborate in this talk. In the corresponding paper, we also look at s- circulant graphs, which we define and discovered while searching for lower bounds of the Cartesian product graphs mentioned earlier.
Kara Schatz - The Linear Bandwidth of Km,n and Kl,m,n, Advisor Dr. Eric Bucher
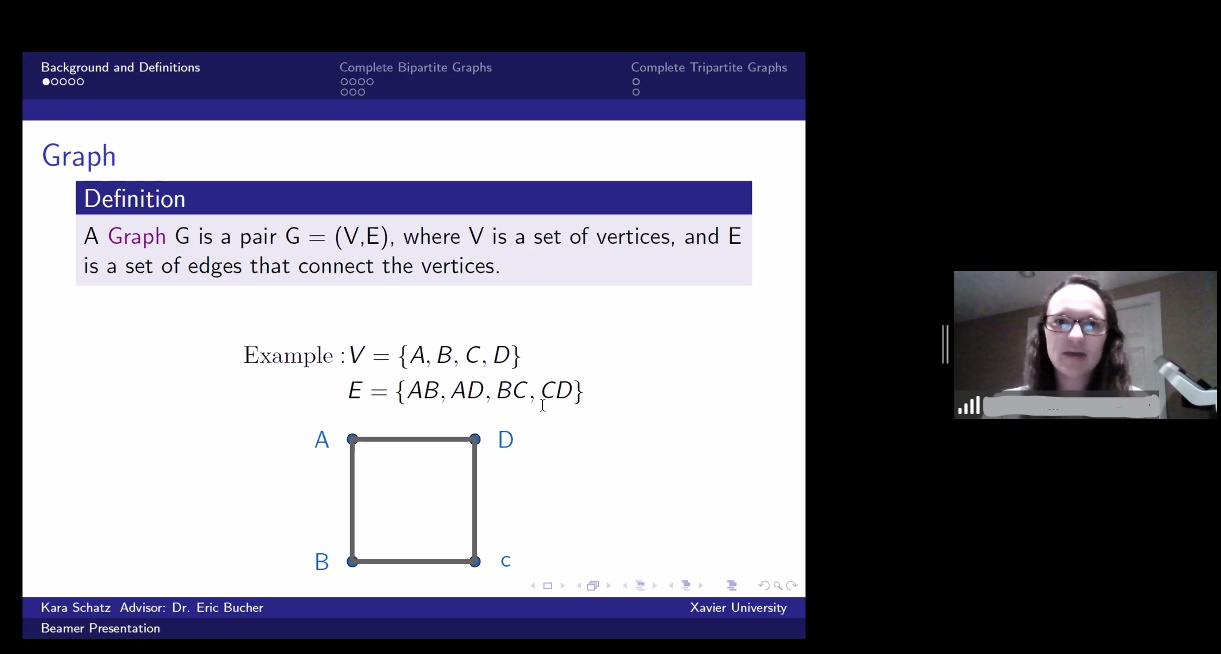
In this talk, we address the problem of determining the linear bandwidth of graphs, which is an NP-complete problem. However, it is possible to compute the linear bandwidth for certain classes of graphs, such as complete bipartite and complete tripartite graphs, which is one of the central goals of this talk. First, we will determine and prove a formula for the linear bandwidth of complete bipartite graphs. Then, we will turn our attention to determining bandwidth criticality. A graph is bandwidth critical if all of its subgraphs would necessarily have a smaller bandwidth. We give a classification of which complete bipartite graphs have this characteristic. Then, we provide the same information on complete tripartite graphs with less detail.
Patrick Simpson - The Optimal NBA Roster-Building Strategy, Advisor Dr. Max Buot
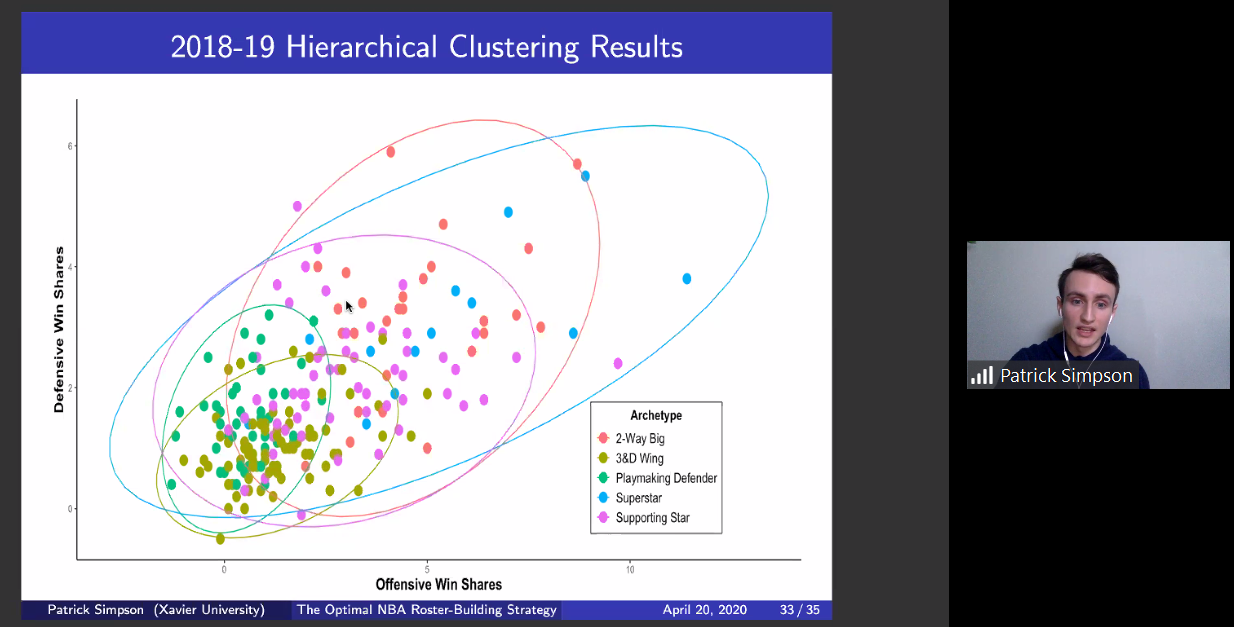
Executives in the National Basketball Association customarily emulate the roster-building strategy of successful franchises. While a superstar is the foundation of a team, marginal advantages propel it to championship contention. One way an organization can gain an edge is through shrewd roster management. In this project, hierarchical clustering is used to group players by ability. After clusters are created, we investigate which players are similar. With this intel, we can make sound decisions regarding team construction.
Duncan Webb - The Use of Oncolytic Viruses in Tumor Therapy, Advisor Dr. Hem Raj Joshi
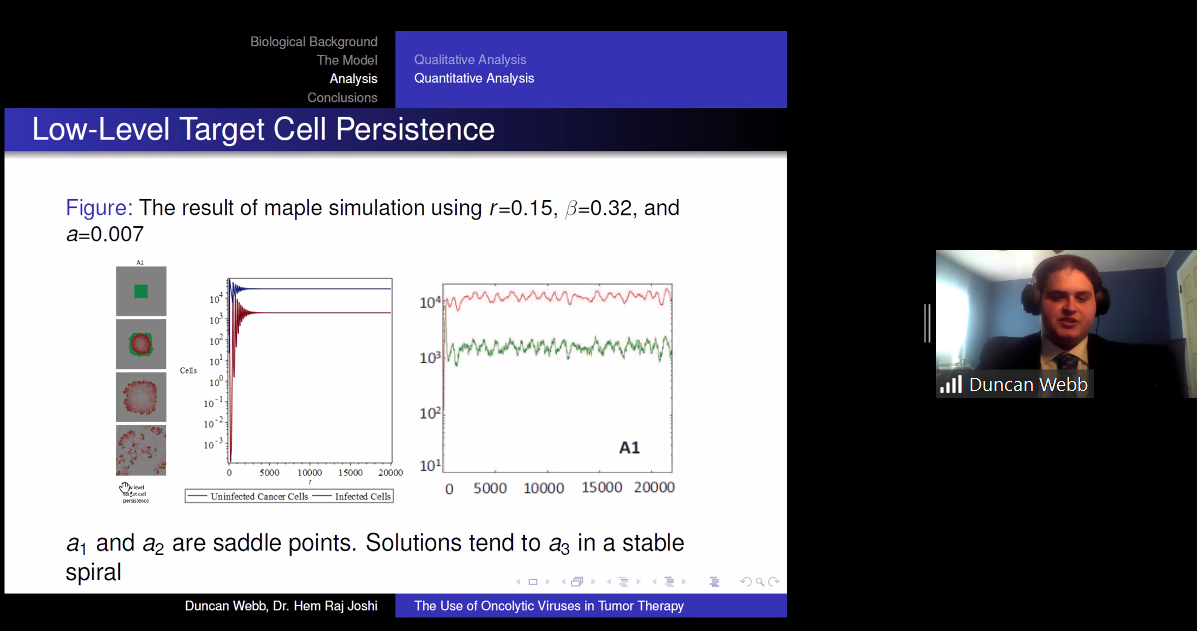
Cancer is a term used for classification of diseases in which abnormal cells divide without control and invade other tissues. Cancer cases have been at an all time high as of 2020, with an estimated 1.7 million new cases in 2019 alone. Due to the severity and lethality of this type of disease, many billions of dollars have been invested in finding a cure, but one has yet to be obtained. A newer form of tumor therapy to help with the disease is being researched currently, called Oncolytic Virus Tumor Therapy. An oncolytic virus is one which specifically targets cancerous cells using proteins which express themselves on the outside of only cells which are infected with cancer. In this presentation we will explore a simple oncolytic virus therapy model created by Wodarz to model an agent-based system where no spatial restrictions are in place, infection interactions are driven by the laws of mass-action, and all simulations take place in a simple in-vitro environment. We will explore the behavior of this model using standard quantitative and qualitative analysis techniques which aim to show that this simple ordinary differential equations model can be used to model a spatially sensitive environment.